Description Logics
Human Reasoning
2013-11-08
Introduction
Ontology
An ontology is a specification of a conceptualization. That is, an ontology is a description (like a formal specification of a program) of the concepts and relationships that can exist for an agent or a community of agents. [...] My colleagues and I have been designing ontologies for the purpose of enabling knowledge sharing and reuse. [Gruber, 1992]
- Individuals / Objects
- Classes / Sets / Concepts
- Relations
- The semantic web, Web 3.0, RDF, OWL, OWL-DL, etc...
SNOMED-CT
- Systematized Nomenclature Of Medicine Clinical Terms
Snomed CT är ett internationellt begreppssystem som syftar till att göra dokumentationen i vård och omsorg enhetlig, entydig och ändamålsenlig. [...] Målet är att Snomed CT ska användas inom vård och omsorg i hela landet. [Socialstyrelsen]
- Concept1 - Relation - Concept2
- Common Cold - causative agent - Virus
- \(\mathtt{CommonCold}(x) \rightarrow \exists y (\mathtt{causativeAgent}(x,y) \land \mathtt{Virus}(y))\)
- \(\mathtt{CommonCold} \sqsubseteq \exists \mathtt{causativeAgent}. \mathtt{Virus}\)
- Based on a description logic.
- Used in so called Clinical decision support system (CDSS).
Formal definitions
Syntax
ALC - Attributive Concept Language with Complement
- The set of concepts is built up from atomic concepts \(A\) and roles \(R\): \[C ::=A \mathbin\vert \top \mathbin\vert \bot \mathbin\vert \lnot C \mathbin\vert C \sqcup C \mathbin\vert C \sqcap C \mathbin\vert \exists R.C \mathbin\vert \forall R.C\] where \(A\) is an atomic concept and \(R\) a role.
- The set of formulas is defined by: \[ \varphi ::= C \equiv C \mathbin\vert C \sqsubseteq C \mathbin\vert C \] where \(C\) is a concept.
- No individual variables!
- \(\exists R. C\) "All things with an \(R\)-successor in \(C\)". "R some C"
- \(\forall R. C\) "All things with all \(R\)-successors in \(C\)". "R all C"
Examples
- \(\mathtt{Male} \sqsubseteq \mathtt{Person}\)
- \(\exists \mathtt{hasChild}.\mathtt{Male}\)
- \(\forall \mathtt{hasChild}.\mathtt{Male}\)
- \(\exists \mathtt{hasChild}.\mathtt{Male} \sqcap \forall \mathtt{hasChild}.\mathtt{Male}\)
Semantics
- A model \(M\) gives an interpretation to each atomic concept and role.
- By a recursive definition each concept \(C\) is given an interpretation \(C^M \subseteq M\).
- \(\top^M = M\) and \(\bot^M = \emptyset\)
- \((C \sqcup D)^M = C^M \cup D^M\).
- \((C \sqcap D)^M = C^M \cap D^M\).
- \((\lnot C)^M = M \setminus C^M\).
- \((\forall R.C)^M = \{a \in M | \forall x \in M (\langle a,x\rangle \in R^M \rightarrow x \in C^M) \}\)
- \((\exists R.C)^M = \{a \in M | \exists x \in M (\langle a,x\rangle \in R^M \land x \in C^M) \}\)
Semantics continued
- \(M \models C \sqsubseteq D\) iff \(C^M \subseteq D^M\).
- \(M \models C \equiv D\) iff \(C^M = D^M\).
- \(O \models \varphi\) if all models of \(O\) are models of \(\varphi\).
- \(\models \varphi\) if all models are models of \(\varphi\).
A concept \(C\) is satisfiable if there is a model \(M\) such that \(C^M \neq \emptyset\).
\(C\) is satisfiable iff \(\not\models C \sqsubseteq \bot\).
Examples
- \(\mathtt{Person} \sqsubseteq \lnot\mathtt{Movie}\)
- \(\mathtt{RRated} \sqsubseteq \mathtt{Movie}\)
- \(\mathtt{RRated} \equiv \mathtt{Thriller} \sqcup (\forall \mathtt{hasViolenceLevel}.\mathtt{High})\)
- \(\exists \mathtt{hasViolenceLevel}.\top \sqsubseteq \mathtt{Movie}\)
Terminology Box
A TBox is a set \(O\) of formulas of the form \(A \equiv D\) or \(A \sqsubseteq D\) where \(A\) is an atomic concept and each atomic concept occurs at most once on the left hand side of a formula in \(O\).
Sometimes we need the TBox to be acyclic:
An atomic concept \(A\) directly uses an atomic concept \(B\) in \(O\) if \(B\) occurs in the right-hand side of any axiom with \(A\) on the left-hand side. The relation uses is then the transitive closure of the directly uses relation. \(O\) is acyclic if no atomic concept \(A\) uses \(A\).
Assertion Box
An ABox consists of assertions of the form \(C(a)\) and \(R(a,b)\) where \(a\) and \(b\) are constants.
Not included in our simplified system.
An ABox is, in some sense, equivalent to a relational database where we only allow unary and binary relations.
Important: In the context of relational databases we have the closed world assumption. Not so in DL. DL is monotone.
- A pair of a TBox and an ABox is called a Knowledge Base.
Connections with other formalisms
First-order Logic
- Clearly any concept can be rewritten as a formula with a free variable.
\(\forall R_1. (C \sqcap \exists R_2 .C)\) is translated to \[\forall y (R_1(x,y) \rightarrow (C(y) \land \exists z (R_2(y,z) \land C(z))))\]
- ALC translates in this way into a small fragment of FOL.
- ALC can be translated into FO². (Sat is NEXPTIME)
- ALC can be translated into GF.
Modal propositional logic
ALC is multi modal logic K:
- \(\forall R\) translates to \(\Box_R\)
- \(\exists R\) translates to \(\Diamond_R\)
- \(\sqcup\) to \(\lor\)
- \(\sqcap\) to \(\land\)
- \(\lnot\) to \(\lnot\)
Complexity
Explanations
Intro
An engineer developing an ontology \(O\) suddenly realizes that \(O \models \top \sqsubseteq \bot\). (debugging)
A medical doctor gets a recommended treatment relying on a medical ontology, such as SNOMED-CT. (safety)
Actually, it follows from SNOMED-CT that \(\mathtt{AmpOfFinger} \sqsubseteq \mathtt{AmpOfHand}\).
Why does an entailment \(O \models \varphi\) hold?
Proofs
- Several proof system for DL.
- Usually based on tableaux systems. (Not very surprising, remember ALC `is' multi modal K.)
- These systems are constructed to get fast automatic theorem provers (called reasoners in the DL-community).
- They are not well suited as explanations for humans.
Justifications
A justification of \(\varphi\) (wrt \(O\)) is a minimal subset \(I \subseteq O\) such that \(I \models \varphi\).
Example:
is a justification for \(\mathtt{RRated} \sqsubseteq \mathtt{Movie}\).
- \(\mathtt{RRated} \sqsubseteq \mathtt{Thriller}\)
- \(\mathtt{Thriller} \sqsubseteq \mathtt{Movie}\)

- \(\mathtt{Person} \sqsubseteq \lnot\mathtt{Movie}\)
- \(\mathtt{RRated} \sqsubseteq \mathtt{Movie}\)
- \(\mathtt{RRated} \equiv \mathtt{Thriller} \sqcup (\forall \mathtt{hasViolenceLevel}.\mathtt{High})\)
- \(\exists \mathtt{hasViolenceLevel}.\top \sqsubseteq \mathtt{Movie}\)
is a justification for \(\mathtt{Person} \sqsubseteq \bot\).
Lemmatized justifications
[Horridge, Parsia, Sattler]
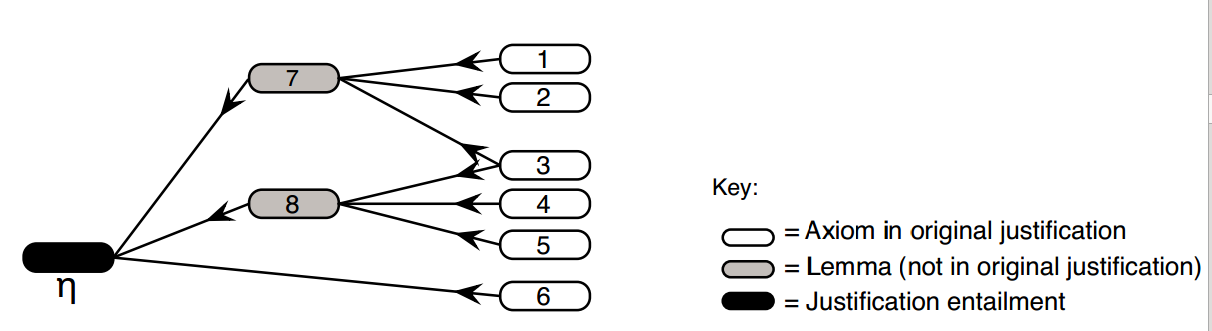
The definition rests on a notion of complexity measure.
Complexity measure
- What is the complexity of an entailment \(I \models \varphi\)?
- We want to model cognitive complexity.
- The naïve approach of Horridge et al:
The complexity of an entailment \(I \models \varphi\) is the sum of a number of complexity scores.
The complexity scores are syntactic and semantic scores such as:
- 100 times the number of axiom types in \(I,\varphi\).
- 10 times the number of constructors in \(I,\varphi\).
A better way
- Use a natural proof system somehow based on a cognitive model.
- Define the complexity of an entailment as the length of the shortest proof.
- The proof system should be:
- Linear
- Local
- Deep
A natural proof system
- Rules, for example:
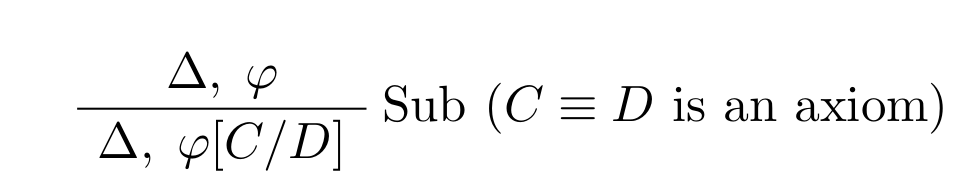
- Axioms, such as: \(C \sqcup \lnot C \sqsubseteq \top\)
- Cognitive Restrictions that correspond to bounded working memory.
An example proof

Results
- A procedure for finding the shortest proof was implemented in Haskell by Abdul Rahim Nizamani.
- A small experiment was reported on in the Horridge et al paper. 14 participants.
| Justification | Success rate | Model complexity | Proof length |
|---|---|---|---|
| 1 | 57% | 654 | 11 |
| 2 | 57% | 703 | 14 |
| 3 | 29% | 675 | 18 |
But hey!
Why can't we extract explanations directly from the proofs?
Thank you
These slides were made using: